Points Where Tangent Line Is Horizontal Calculator

A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Therefore, when the derivative is zero, the tangent line is horizontal.

To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus. The geometrical idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculus in the 17th century. Tangent lines are straight lines that pass through a given curve and have the slope of the curve at the point where they intersect.

The idea of tangent lines can be extended to higher dimensions in the form of tangent planes and tangent hyperplanes. A normal line is a line that is perpendicular to the tangent line or tangent plane. Wolfram|Alpha can help easily find the equations of tangents and normals to a curve or a surface. The slope calculator determines the slope or gradient between two points in the Cartesian coordinate system.

The slope is basically the amount of slant a line has and can have a positive, negative, zero, or undefined value. Before using the calculator, it is probably worth learning how to find the slope using the slope formula. To find the equation of a line for any given two points that this line passes through, use our slope intercept form calculator. The formulas above fail when the point is a singular point.

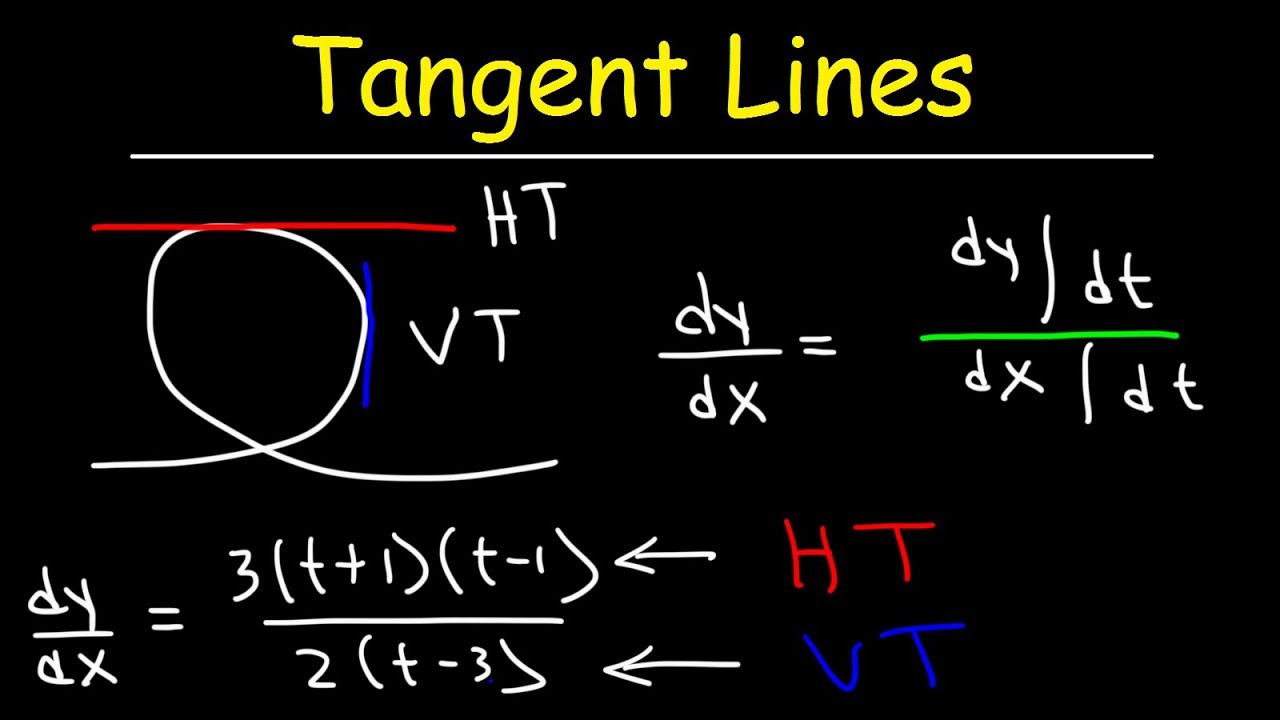
In this case there may be two or more branches of the curve that pass through the point, each branch having its own tangent line. Since any point can be made the origin by a change of variables this gives a method for finding the tangent lines at any singular point. Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents.

Using implicit differentiation find y', so that you have a formula for slopes of tangent lines to the graph of the original function. The slope formula is useful for points along a linear line, but when working with non-linear functions you might need to use an average rate of change calculator. In addition to finding the area under a parametric curve, we sometimes need to find the arc length of a parametric curve.

In the case of a line segment, arc length is the same as the distance between the endpoints. If a particle travels from point A to point B along a curve, then the distance that particle travels is the arc length. To develop a formula for arc length, we start with an approximation by line segments as shown in the following graph. These points correspond to the sides, top, and bottom of the circle that is represented by the parametric equations (Figure 7.19). On the left and right edges of the circle, the derivative is undefined, and on the top and bottom, the derivative equals zero. To find the equation of a tangent line, sketch the function and the tangent line, then take the first derivative to find the equation for the slope.

Enter the x value of the point you're investigating into the function, and write the equation in point-slope form. Check your answer by confirming the equation on your graph. The tangent at A is the limit when point B approximates or tends to A.

To determine the equation of a tangent, we need to know the slope of the line as well as the point where it touches the curve. If we take the first-order derivative of the given function and evaluate it at the point of intersection, we can find the slope of a tangent. Suppose we know the function of the curve, f, that the tangent touches and the x coordinate, x1, of the point of intersection. Then we can follow the steps given below to find the equation of the tangent.

Tangent Line Calculator is an online tool that helps to find the equation of the tangent line to a given curve when we know the x coordinate of the point of intersection. The point-slope form of a line can be used to find the equation of a tangent. To use the tangent line calculator, enter the values in the given input boxes.

Knowing the slopes of tangent lines at various points on the graph of a function can help one better understand the graph of the overall function. When studying mathematics functions and methodology of calculation, a good place to start is understanding the significance of one-sided limits and continuity. Learn more about the properties and functions, and study an example of a formula for finding one-sided limits and continuity. Once you have the slope of the tangent line, which will be a function of x, you can find the exact slope at specific points along the graph. A horizontal tangent line is parallel to the x-axis and shows where a function has a slope of zero. You can find these lines either by looking at a graph or by setting an equation to zero to find maximums and minimums.

A stationary point of a function $f$ is a point where the derivative of $f$ is equal to 0. These points are called "stationary" because at these points the function is neither increasing nor decreasing. Graphically, this corresponds to points on the graph of $f$ where the tangent to the curve is a horizontal line.

It is worth mentioning that any horizontal line has a gradient of zero because a horizontal line has the same y-coordinates. This will result in a zero in the numerator of the slope formula. On the other hand, a vertical line will have an undefined slope since the x-coordinates will always be the same. This will result the division by zero error when using the formula. Differentiate the equation of the circle and plug in the values of x,y in the derivative. Use the slope-point form of the line to find the equation, with the slope you obtained earlier and the coordinates of the point.

Unlike a straight line, a curve's slope constantly changes as you move along the graph. To find the equation for the tangent, you'll need to know how to take the derivative of the original equation. The tangent plane to a surface at a given point p is defined in an analogous way to the tangent line in the case of curves. This result is the equation of the tangent line to the given function at the given point. When we have a function that isn't defined explicitly for ???

In mathematics, slopes and tangents help determine ratios and rates of change. Learn how to show slopes and tangents as lines on a graph, explore the concept of slope as it pertains to hills, and recognize how slope can be used to describe steepness. Newton's method (also called the Newton–Raphson method) is a way to find x-intercepts of functions. In other words, you want to know where the function crosses the x-axis. The method works well when you can't use other methods to find zeros of functions, usually because you just don't have all the information you need to use easier methods.

Points Where The Tangent Line Is Horizontal While Newton's method might look complex, all you're actually doing is finding a tangent line, then another tangent line, and repeat, until you think you're close enough to the actual solution. The first derivative test determines the nature of a stationary point $x$ by evaluating the sign of the first derivative at points $x+\epsilon$ and $x-\epsilon$, where $\epsilon\ll1\in\mathbb$. This determines whether the function is increasing or decreasing at these points, thus indicating the shape of the graph. The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′.

The derivative of a function has many applications to problems in calculus. It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values. This video explains how to determine the points on a polar curve where there are horizontal and vertical tangent lines.

The slopes of lines are important in determining whether or not a triangle is a right triangle. If any two sides of a triangle have slopes that multiply to equal -1, then the triangle is a right triangle. The computations for this can be done by hand or by using the right triangle calculator.

You can also use the distance calculator to compute which side of a triangle is the longest, which helps determine which sides must form a right angle if the triangle is right. 🙋 To find the gradient of non-linear functions, you can use the average rate of change calculator. Since the tangent line touches the circle at just one point, we will never be able to calculate its slope directly, using two "known" points on the line.

What we need is a way to capture what happens to the slopes of the secant lines as they get "closer and closer" to the tangent line. Use our free online calculator to solve challenging questions. With Cuemath, find solutions in simple and easy steps. A tangent line in an ininflection point does cross the graph of the function. This applet illustrates the computation of the normal line and the tangent plane to a surface at a point.

The derivative of a function is a function that for every point gives the slope of the graph of the function. You can easily see why you need to know the slope, as well as the coordinates of the point of tangency to uniquify the tangent line. The calculator will find the tangent line to the explicit, polar, parametric and implicit curve at the given point, with steps shown. Anyway, the red line is obviously the tangent in the point (0|0), having the same slope as the graph.

A tangent is a line that intersects a curve at only one point and does not pass through it, such that its slope is equal to the curve's slope at that point. To find a horizontal tangent, you must find a point at which the slope of a curve is zero, which takes about 10 minutes when using a calculator. So in this sense, calling it a tangent line seems reasonable. However, the red line also intersects the curve in two places, which suggests the reverse if we adhere to the old geometric definition of a tangent line. Understanding the nature of slopes of tangent lines to functions can raise red flags when appropriate to alert us to not be so quick to believe what we see on our calculator screens.

Calculus equations that seek to determine the maximum or minimum value for a given parameter are called optimization problems. Learn about optimization problems through real-world examples/explanations and how to use the six-step method to solve optimization problems in calculus. The fundamental theorem of calculus allows us to calculate indefinite integrals as the anti-derivatives of the original polynomial function. Learn how to calculate indefinite integrals of polynomials through several examples and how to apply a general rule to polynomials with any number of variables.

Well, recall from your Calculus I class that with the second derivative we can determine where a curve is concave up and concave down. We could do the same thing with parametric equations if we wanted to. It is a line which touches a circle or ellipse at just one point.

The square of the length of tangent segment equals to the difference of the square of length of the radius and square of the distance between circle center and exterior point. Length of the tangent from a point can be calculated from circle radius and distance between exterior point and center using this online Tangent of a Circle Calculator. Thus, the equation representing a line using slope-intercept form is the y value of a coordinate on the line is equal to the x value of the coordinate times m, plus the y-intercept b. To find the slope of a line, start by finding 2 points along a line and find their x and y values. The value of x is the horizontal distance of the point from the vertical y-axis, and y is the vertical distance of the point from the horizontal x-axis.

Find equations of the tangent plane and the normal line to the given surface at the specified point. For the following exercises, each set of parametric equations represents a line. Without eliminating the parameter, find the slope of each line. For each of the following parametrically defined plane curves, and locate any critical points on their respective graphs.

What we want is a line tangent to the function at (1, 1/2) -- one that has a slope equal to that of the function at (1, 1/2). The sign in front of the gradient provided by the slope calculator indicates whether the line is increasing, decreasing, constant or undefined. If the graph of the line moves from lower left to upper right it is increasing and is therefore positive.

If it decreases when moving from the upper left to lower right, then the gradient is negative. Just as slope can be calculated using the endpoints of a segment, the midpoint can also be calculated. The midpoint is an important concept in geometry, particularly when inscribing a polygon inside another polygon with the its vertices touching the midpoint of the sides of the larger polygon. This can be obtained using the midpoint calculator or by simply taking the average of each x-coordinates and the average of the y-coordinates to form a new coordinate.

Notice that the slope of a line is easily calculated by hand using small, whole number coordinates. The formula becomes increasingly useful as the coordinates take on larger values or decimal values. We will use the formula to calculate the slope of the line passing through the points and (-2, 10). The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point.

More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal. These methods led to the development of differential calculus in the 17th century. Further developments included those of John Wallis and Isaac Barrow, leading to the theory of Isaac Newton and Gottfried Leibniz.